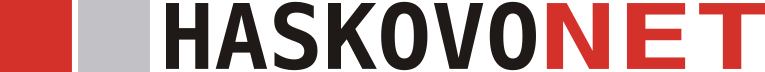Законите на физиката предполагат, че потокът на времето е илюзия. За да избегнем това заключение, може да се наложи да преосмислим реалността на безкрайно точните числа.
Странното е, че макар да имаме усещането, че се движим във времето по границата между фиксираното минало и отвореното бъдеще, тази граница - настоящето, не фигурира никъде в съществуващите закони на физиката.
В теорията на относителността на Алберт Айнщайн например времето е преплетено с трите измерения на пространството, образувайки огъващ се четириизмерен пространствено-времеви континуум - "блокова вселена", обхващаща цялото минало, настояще и бъдеще. Уравненията на Айнщайн изобразяват всичко в блоковата вселена като решено от самото начало; началните условия на космоса определят това, което ще се случи по-късно, и изненади не се случват - те само изглеждат.
"За нас, вярващите физици", пише Айнщайн през 1955 г., седмици преди смъртта си, "разграничението между минало, настояще и бъдеще е само упорито поддържана илюзия."
Лишеният от "време" възглед за една предопределена реалност, поддържан от Айнщайн, остава популярен и днес.
"Мнозинството от физиците вярват във възгледа за блоковата вселена, защото той е предсказан от Общата теория на относителността", коментира Марина Кортес (Marina Cortês), космолог от Лисабонския университет в статия на The Atlantic. "Но , ако някой се замисли малко по-задълбочено за значението на блоковата вселена, той започва да се съмнява и да се колебае относно последиците".
Блоковата вселена
Според теорията на блоковата вселена, Вселената е гигантски блок от всички неща, които някога се случват по всяко време и на всяко място. От тази гледна точка миналото, настоящето и бъдещето всички съществуват — и са еднакво реални.
Как може да си го представим?
Блокът има четири измерения: три пространствени измерения - да речем дължина, височина и ширина - плюс четвърто времево измерение или време. Или нека го направим по-лесно, като визуализираме блоковия модел на нашия свят като триизмерен правоъгълник или паралелепипед.
Две от измеренията на този паралелепипед (да кажем височина и ширина) представляват две от трите пространствени измерения на Вселената.
Третото пространствено измерение в горната схема се пропуска - дължината на паралелепипеда - и се заменя с времето. В единия край на паралелепипеда е Големият взрив. В другия е последният момент от Вселената.
Паралелепипедът е изпълнен с всяко събитие, което някога се е случило, се слува или ще се случи. Разположението на тези събития в паралелепипеда, представлява тяхното местоположение в пространство-времето. Всички събития, включително вашето раждане и смърт, и точно този момент, докато четете тези думи, съществуват някъде в блока.
От наша гледна точка изглежда, че времето тече. Но в модела на блоковата вселена времето не тече.
С други думи, в блоковата вселена няма конкретен настоящ момент, а „миналите“ и „бъдещите“ моменти са относителни. Вие, докато четете това, наистина можете да кажете "аз съм тук", въпреки че вашето "тук" е различно от моето.
При модела на блоковата вселена, разговорът за „настоящето“ или „сега“ работи точно както разговорът за „тук“.
Тъй като винаги се намираме там, където се намираме (това е тривиална истина), всеки се намира в настоящето, точно както всеки се намира на мястото, което нарича „тук“.
Физиците, които анализират внимателно времето, посочват проблемите, породени от квантовата механика - законите, описващи вероятностното поведение на частиците. В квантовия мащаб настъпват необратими промени, които разграничават миналото от бъдещето: Една частица поддържа едновременни квантови състояния, докато не я измерите, и тогава тя приема едно от състоянията. Мистериозно е, че резултатите от отделните измервания са случайни и непредсказуеми, въпреки че поведението на частиците в съвкупност следва статистически модели. Това очевидно несъответствие между естеството на времето в квантовата механика и начина, по който то функционира в теорията на относителността, създава несигурност и объркване.
През изминалата година швейцарският физик Никола Жизен (Nicolas Gisin) публикува четири статии, в които се опитва да разсее мъглата около времето във физиката. Според Жизен проблемът през цялото време е бил математически. Жизен твърди, че времето като цяло и времето, което наричаме настояще, лесно се изразяват на един вековен математически език, наречен интуиционистка математика, която отхвърля съществуването на числа с безкрайно много цифри.
Интуиционистката математика
Интуиционизмът е съвкупност от философски и математически възгледи, които разглеждат математическите съждения от гледна точка на "интуитивната убедителност".
Интуиционистката математика отхвърля подхода на класическата теория на множествата и редица разсъждения на класическата логика. Абстракцията на потенциалната осъществимост, която се използва в интуиционистката математика, е по-близка до реалността, отколкото абстракцията на актуалната безкрайност.
Когато интуиционистката математика се използва за описване на еволюцията на физическите системи, тя ясно показва според Жизен, че "времето наистина тече и се създава нова информация". Нещо повече, с този формализъм строгият детерминизъм, заложен в уравненията на Айнщайн, отстъпва място на непредсказуемост, подобна на квантовата.
Ако числата са крайни и ограничени в своята прецизност, то самата природа по своята същност става неточна и следователно непредсказуема.
Физиците все още усвояват работата на Жизин - не се случва често някой да се опитва да преформулира законите на физиката на нов математически език - но много от тези, които са се запознали с аргументите му, смятат, че те потенциално могат да преодолеят концептуалната пропаст между детерминизма на Общата теория на относителността и присъщата случайност в квантовия мащаб.
"Намирам го за интригуващо", заявява Никол Юнгер Халпърн (Nicole Yunger Halpern), учен в областта на квантовата информация в Харвардския университет, в отговор на неотдавнашната статия на Жизен в Nature Physics. "Готова съм да дам шанс на интуиционистката математика."
Кортес нарича подхода на Жизен "изключително интересен" и "шокиращ и провокативен" по отношение на последиците от него. "Това е наистина много интересен формализъм, който се занимава с този проблем на крайната точност в природата", отбелязва Кортес.
Според Жизен е важно да се формулират закони на физиката, които поставят бъдещето като отворено, а настоящето като много реално, защото точно това изпитваме.
"Аз съм физик, който е стъпил на земята", коментира той. "Времето тече - всички знаем това."
Информация и време
67-годишният Жизен е преди всичко експериментатор. Ръководи лаборатория в Женевския университет, в която са проведени революционни експерименти в областта на квантовата комуникация и квантовата криптография. Но той е и от рядко срещаните физици, който е известен с важни теоретични прозрения, особено такива, свързани с квантовата случайност и нелокалност.
Жизен има навика да размишлява върху дълбоки концептуални загадки. В една неделя преди около пет години той осъзнава, че детерминистичната картина на времето в теорията на Айнщайн и останалата част от "класическата" физика неявно предполага съществуването на неограничена информация.
Да разгледаме метеорологичното време. Тъй като то е хаотично или силно чувствително към малки разлики, не можем да предвидим точно какво ще бъде времето след седмица. Но тъй като това е класическа система, учебниците ни казват, че по принцип бихме могли да предскажем времето след седмица, стига да успеем да измерим достатъчно точно всеки облак, порив на вятъра и всяко размахване на крило на пеперуда. Сами сме си виновни, че не можем да измерваме условията с достатъчно знаци след десетичната запетая, за да екстраполираме напред и да правим съвършено точни прогнози, защото реалната физика на времето се развива като часовников механизъм, нали?
Сега да разширим тази идея до цялата Вселена. В един предопределен свят, в който сякаш потокът на времето е само илюзия, всичко, което ще се случи за цялото време, всъщност е трябвало да бъде зададено от самото начало, като началното състояние на всяка една частица е кодирано с безкрайно много цифри точност. В противен случай в далечното бъдеще щеше да настъпи момент, когато самата вселена с часовников механизъм ще "се счупи".
Но информацията е нещо физическо. Съвременните изследвания показват, че тя изисква енергия и заема пространство. Известно е, че всеки обем от пространството има краен информационен капацитет (като най-плътното възможно съхранение на информация се случва в черните дупки). Първоначалните условия на Вселената, осъзнава Жизен, биха изисквали твърде много информация, натъпкана в твърде малко пространство.
Кредит: view.ca
"Реално число с безкрайно много знаци не може да има физически смисъл", отбелязва Жизен.
Блок-вселената, която неявно предполага съществуването на безкрайна информация, би трябвало да се разпадне. И Жизен търси нов начин за описание на времето във физиката, който не предполага безкрайно точно познаване на началните условия.
Логиката на времето
Сега се приема, че съществува континуум (непрекъснатост) от реални числа, повечето от които с безкрайно много цифри след десетичната запетая, няма почти никакви следи от ожесточените дебати по този въпрос през първите десетилетия на XX век. Давид Хилберт, великият немски математик, застъпва станалия днес стандартен възглед, че реалните числа съществуват и могат да бъдат манипулирани като завършени същности. Срещу това схващане се изправят математическите "интуиционисти", водени от известния холандски тополог Лойцен Егбертус Ян Брауер, който вижда математиката като конструкт. Брауер настоява, че числата трябва да могат да се конструират, техните цифри да се изчисляват, избират или определят на случаен принцип една по една. Числата са крайни, казва Брауер, и също така са процеси: Те могат да стават все по-точни, тъй като все повече цифри се разкриват в така наречената от него последователност на избора - с помощта на функция, даваща стойности с все по-голяма точност.
Обосновавайки математиката с това, което може да бъде конструирано, интуиционизмът поражда далечни последици за практиката на математиката и за определянето на това кои твърдения могат да се смятат за верни. Най-радикалното отклонение от стандартната математика се оказва, не е в сила законът за изключеното трето, възхваляван принцип още от времето на Аристотел. Законът за изключеното трето гласи, че или дадено твърдение е истинно, или отрицанието му е истинно - ясен набор от алтернативи, който предлага мощен инструмент за построяване на изводи. Но в концепцията на Брауер твърденията за числата могат да бъдат нито верни, нито неверни в даден момент, тъй като точната стойност на числото все още не е ясна.
Тя не се различава от стандартната математика, когато става въпрос за числа като 4, ½ или π - отношението на обиколката на кръг към неговия диаметър. Въпреки че π е ирационално число, което няма крайно десетично разширение, съществува алгоритъм за генериране на десетичното му разширение, което прави π също толкова детерминирано, колкото и число като ½. Но да разгледаме друго число x, което е близко до ½.
Да кажем, че стойността на х е 0.4999, където следващите цифри се появяват в последователност от избори. Възможно е поредицата от деветки да продължи вечно и тогава x ще се стрими към ½. (Този факт, че 0.499(9) = 0.5, е верен и в стандартната математика, тъй като x се различава от ½ с по-малко от всяко крайно число.)
Но ако в някакъв бъдещ момент в тази последователност се появи цифра, различна от 9 - ако, да допуснем, стойността на x стане 4.999999999999997... - тогава независимо какво ще се случи след това, x ще бъде по-малко от ½. Но до момента, когато знаем само 0,4999, "не знаем дали някога ще се появи цифра, различна от 9", обяснява Карл Пози (Carl Posy), математик философ в Еврейския университет в Йерусалим и водещ експерт по интуиционистка математика. "В момента на изучаване на това x, не можем да кажем, че x е по-малко от ½, нито пък можем да кажем, че x е равно на ½." Твърдението "x е равно на ½" не е вярно, както и негово отрицанието му. Законът за изключеното трето не работи.
Освен това континуумът не може да бъде ясно разделен на две части, едната от които да се състои се от всички числа, по-малки от ½, и всички числа, по-големи или равни на ½. "Ако се опитате да разрежете континуума наполовина, това число х ще се залепи за ножа и няма да е нито отляво, нито отдясно", обяснява Пози. "Континуумът се оказва пластичен и лепкав."
Хилберт сравнява отстраняването на закона за изключеното трето от математиката със "забрана на боксьора да използва юмруците си", тъй като този принцип е в основата на голяма част от математическите дедукции. Макар че интуиционистката рамка на Бруер очарова такива хора като Курт Гьодел и Херман Вайл, стандартната математика с нейните реални числа доминира днес заради лесната си употреба.
За първи път Жизен се сблъсква с интуиционистката математика на конференция през май 2019 г. , на която присъства и Пози. Когато двамата започват да разговарят, Жизен бързо вижда връзката между разгръщащите се десетични цифри на числата в тази математическа рамка и физическото понятие за време във Вселената. Материализиращите се цифри сякаш естествено съответстват на последователността от моменти, определящи настоящето, когато несигурното бъдеще се превръща в конкретна реалност. Отсъствието на закона за изключеното трето е подобна на недетермизма на бъдещето.
В работата си, публикувана през декември 2019 г. във Physical Review A, Жизен и неговият сътрудник Флавио Дел Санто (Flavio Del Santo) използват интуиционистка математика, за да формулират алтернативна версия на класическата механика, която прави същите прогнози като стандартните уравнения, но представя събитията като недетерминирани - създавайки картина на вселена, в която се случва неочаквано и времето се развива.
Това напомня ситуацията с метеорологичното време - не можем да прогнозираме точно времето, защото са ни неизвестни началните условия на всеки атом на Земята с безкрайна точност. Но в индетерминистичния вариант на развитие на собитията на Жизен тези точни числа изобщо не съществуват. Интуиционистката математика отразява това: Цифрите, които определят все по-точно състоянието на времето и диктуват развитието му все по-напред в бъдещето, се избират в реално време, докато това бъдеще се развива в последователност от избори. Ренато Рене (Renato Renner), квантов физик от Швейцарския федерален технологичен институт в Цюрих, заявява, че аргументите на Жизен "сочат, че детерминистичните прогнози са фундаментално невъзможни като цяло".
С други думи, светът е недетерминистичен, бъдещето е отворено. Времето, казва Жизен, "не се развива като кинолента. То наистина представлява творческо развитие. Новите цифри наистина се пораждат с течение на времето."
Фей Даукър (Fay Dowker), теоретик на квантовата гравитация в Имперския колеж в Лондон, споделя, че тя "много симпатизира" на аргументите на Жизен, тъй като "той е на страната на онези от нас, които смятат, че физиката не съответства на нашия опит и следователно нещо изпускаме". Даукър е съгласна, че математическите езици оформят разбирането ни за времето във физиката и че стандартната хилбертова математика, която разглежда реалните числа като завършени същности, "определено е статична. Нейната характерна черта е безвремието и това определено ни ограничава като физици, когато се опитваме да включим нещо, което е толкова динамично, като нашето усешане за потока на времето."
За физици като Даукър, които се интересуват от връзките между гравитацията и квантовата механика, едно от най-важните последствия от този нов възглед за времето е как то започва да свързва два дълго време смятани за взаимно несъвместими възгледа за света.
"Едно от последствията лично за мен е, че класическата механика в някои отношения е по-близо до квантовата механика, отколкото сме си мислили", отбелязва Рене.
Квантовата неопределеност и времето
Ако физиците искат да разгадаят мистерията на времето, те трябва да се справят не само с пространствено-времевия континуум на Айнщайн, но и с това, че Вселената е фундаментално квантова и се управлява от вероятности и неопределеност. Квантовата теория описва много различна картина на времето от теорията на Айнщайн.
"Нашите две големи теории за физиката - квантовата теория и Общата теория на относителността - изказват различни твърдения", отбелязва Рене.
Той и няколко други физици твърдят, че това несъответствие е в основата на усиленото търсене на квантова теория на гравитацията - описание на квантовия произход на пространство-времето - и на разбиране на причините за Големия взрив.
"Ако разгледаме всички парадокси и проблеми, в крайна сметка те винаги се свеждат до това понятие за време."
В квантовата механика времето е твърдо, а не се огъва и не се преплита с измеренията на пространството, както е в теорията на относителността. Освен това измерванията на квантовите системи "правят времето в квантовата механика необратимо, а в теорията на относителността - напълно обратимо", обяснява Рене. "Така че времето играе в това роля, която все още не разбираме напълно."
Много физици тълкуват квантовата физика като доказателство, че Вселената е недетерминирана. "За Бога, имате два атома уран: Единият от тях се разпада след 500 години, а другият - след 1000 години, и въпреки това са напълно идентични във всяко едно отношение", коментира Нима Аркани-Хамед (Nima Arkani-Hamed), физик в Института за напреднали изследвания в Принстън, Ню Джърси. "Във всеки значим смисъл Вселената не е детерминирана."
Все пак други популярни интерпретации на квантовата механика, включително интерпретацията на многото светове, успяват да запазят жива класическата, детерминистична представа за времето. В тези теории квантовите събития се разиграват в рамките на предопределената реалност. Според теорията за вултивселената например всяко квантово измерване разделя света на множество разклонения, които реализират всички възможни резултати, всички те са предварително зададени.
Идеите на Жизен са в друга посока. Вместо да се опитва да превърне квантовата механика в детерминистична теория, той се надява да осигури общ недетерминистичен език за класическата и квантовата физика. Но подходът се отклонява от стандартната квантова механика в важен аспект.
В квантовата механика информацията може да бъде разбъркана или кодирана, но никога не може да бъде създадена или унищожена. И все пак, ако цифрите на числата, определящи състоянието на Вселената, нарастват с течение на времето, както предлага Жизен, тогава се появява нова информация. Жизен заявява, че "абсолютно" отхвърля схващането, че информацията се запазва в природата, главно защото "очевидно има нова информация, която се създава по време на процеса на измерване". "Искам да кажа, че имаме нужда от нов начин да погледнем на тези идеи", добавя Жизен.
Този нов начин на мислене за информацията може да разреши информационния парадокс на черната дупка - какво се случва с информацията, погълната от черни дупки. Според Общата теория на относителността черните дупки са неразрушими обекти, а квантовата теория говори за възможността за изпаряване на черни дупки поради радиация на Хокинг и в този случай се появява парадокс. Ако една различна формулировка на квантовата механика от гледна точка на интуиционистката математика позволява информацията да се създава чрез квантови измервания, ще позволява и информацията да се унищожава.
Джонатан Опенхайм (Jonathan Oppenheim), физик-теоретик от Университетския колеж в Лондон, смята, че информацията наистина се губи в черните дупки. Той не знае дали интуиционизмът на Брауер ще бъде ключът към доказването на това, както твърди Жизен, но според него има основания да се смята, че създаването и унищожаването на информация може да е дълбоко свързано с времето.
"Информацията се унищожава, когато се движим напред във времето, тя не се унищожава, когато се движим в пространството", посочва Опенхайм. Измеренията, които съставляват блоковата вселена на Айнщайн, са много различни едно от друго.
|
Пространствено-времева диаграма на Минковски. Жизен свързва тази лепкавост с усещането ни, че настоящето е "дебело" - ние го смятаме по-скоро реално съществуващ момент, а не просто точка с нулева ширина, която чисто разцепва миналото от бъдещето. |
Наред с подкрепата на идеята за създаващото (и евентуално разрушаващото) време, интуиционистката математика предлага и нова интерпретация на нашия съзнателен опит за времето. Припомнете си, че в тази рамка континуумът е лепкав, невъзможно е да бъде разрязан на две. Жизен свързва тази лепкавост с усещането ни, че настоящето е "дебело" - ние го смятаме по-скоро реално съществуващ момент, а не просто точка с нулева ширина, която чисто разцепва миналото от бъдещето.
В стандартната физика, базирана на стандартната математика, времето е непрекъснат параметър, който може да приеме всякаква стойност на числовата линия. "Обаче", казва Жизен, "ако континуумът е представен от интуиционистката математика, тогава времето не може да бъде рязко разрязано на две." То е плътно, по думите на Жизен "в същия смисъл, в който е медът".
Засега това е само аналогия. Опенхайм заявява, че има "добро усещане за тази идея, че настоящето е гъсто. Не знам откъде идва това усещане."
Бъдещето на времето
Идеите на Жизен предизвикват разнообразни реакции от страна на други теоретици, всеки от които има свои собствени мисловни експерименти и интуиции за времето.
Няколко експерти се обединяват около мнението, че реалните числа изглежда не са физически реални и че физиците се нуждаят от нов формализъм, който не разчита на тях
Ахмед Алмейри (Ahmed Almheiri), физик-теоретик от Института за напреднали изследвания, който изучава черните дупки и квантовата гравитация, смята, че квантовата механика "изключва съществуването на континуум". Квантовата математика групира енергията и други величини в пакети, които приличат повече на цели числа, отколкото на континуум. А безкрайните числа се орязват в черните дупки. "Една черна дупка може да изглежда, че има непрекъснато безкраен брой вътрешни състояния, но [те] се орязват", посочва той, заради ефектите на квантовата гравитация. "Реалните числа не могат да съществуват, защото не може да се скрият вътре в черните дупки. В противен случай те би трябвало да могат да крият там безкрайно количество информация".
Санду Попеску (Sandu Popescu), физик от Бристолския университет, който често си кореспондира с Жизен, е съгласен с индетерминистичния мироглед на Жизен, но казва, че не е убеден, че е необходима интуиционистка математика. Попеску възразява срещу идеята, че цифрите на реалните числа може да се смятат за информация.
Аркани-Хамед смята, че използването на интуиционистката математика от Жизен е интересно и потенциално подходящо за случаи като черните дупки и Големия взрив, при които гравитацията и квантовата механика влизат в очевиден конфликт.
"Тези въпроси - за крайните числа или за нещата, които съществуват в основата си, за това дали съществуват безкрайно много цифри или цифрите се създават в хода на работата", обяснява Аркани-Хамед, "може да са свързани с това как в крайна сметка трябва да разглеждаме космологията в ситуации, в които не знаем как да прилагаме квантовата механика."
Той също смята за необходимо създаването на нов математически език, който би могъл да "освободи" физиците от безкрайната точност и да им позволи да "говорят за неща, които са постоянно малко размити".
Идеите на Жизен намират отклик в много краища на света, но все още се нуждаят от конкретизация. Занапред той се надява да намери начин да преформулира относителността и квантовата механика в термините на крайната, размита интуиционистка математика, както е направил с класическата механика, като по този начин потенциално да сближи тези теории. И вече има някои идеи за това как да подходи към квантовата страна на въпроса.
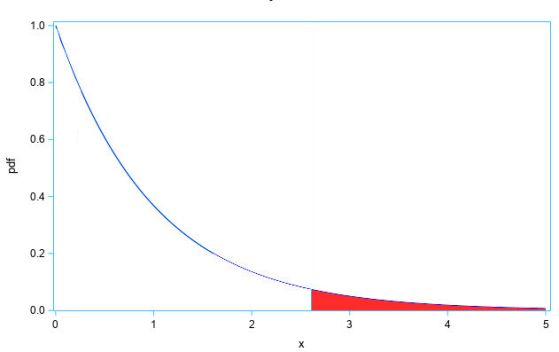
Пример за дълга "опашка" на крива на вероятностно разпределение.
Един от начините, по които безкрайността се появява в квантовата механика, е "проблемът с опашката" (tail problem): Опитайте се да локализирате квантова система, например електрон на Луната, и "ако направите това със стандартната математика, трябва да се признае, че вероятността електронът на Луната да бъде открит и на Земята е изключително малка", посочва Жизен. "Опашката" на математическата функция, обозначаваща позицията на частицата, "става експоненциално малка, но не нулева".
Но Жизин се пита: "Каква реалност трябва да се припише на това свръхмалко число? Повечето експериментатори биха казали: "Считайте го за нула и точка". Но може би по-теоретично ориентираните ще кажат: "Добре, но според математиката там трябва има нещо".
"Обаче всичко зависи от конкретната математика", продължава той. "В класическата математика има нещо. В интуиционистката математика - не. Там няма нищо." Електронът е на Луната и шансът му да се появи на Земята е наистина нулев.
Откакто Жизин публикува работата си, бъдещето става все по-неопределено.
Gisin, N. Mathematical languages shape our understanding of time in physics. Nat. Phys. 16, 114–116 (2020). https://doi.org/10.1038/s41567-019-0748-5
Physics without determinism: Alternative interpretations of classical physics - Flavio Del Santo and Nicolas Gisin, Phys. Rev. A 100, 062107 – Published 5 December 2019 https://journals.aps.org/pra/abstract/10.1103/PhysRevA.100.062107
Does Time Really Flow? New Clues Come From a Century-Old Approach to Math - Natalie Wolchover, Quanta Magazine