Теорията на възлите далеч не е само абстрактен математически куриоз, а е дала тласък на много открития в математиката и извън нея.
Теорията на възлите започва като опит да се разбере фундаменталната структура на Вселената. През 1867 г., когато учените нетърпеливо се опитват да разберат с какво биха могли да се обяснят всички различни видове материя, шотландският математик и физик Питър Гътри Тейт (Peter Guthrie Tait) показва на своя приятел и сънародник сър Уилям Томсън своето устройство за генериране на димни пръстени. Томсън, който по-късно става лорд Келвин (създател на температурната скала), е запленен от примамливите форми на пръстените, тяхната стабилност и взаимодействието им. Вдъхновението му го отвежда в изненадваща посока: Може би, помислил си той, както димните пръстени са вихри във въздуха, така и атомите са възлови вихрови пръстени в светлинния етер - невидима среда, през която, според физиците, се разпространява светлината.

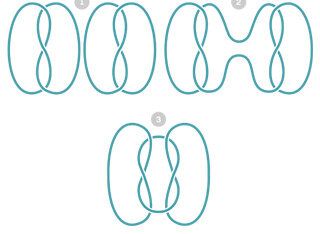
Примери за различни възли, включително тривиалния възел (горе вляво) и трилистника (под него). Кредит: Wikimedia Commons
Макар че тази идея от викторианската епоха днес може да звучи смешно, тя не е била несериозно изследване. Теорията за вихрите имала много основания да бъде препоръчана: Огромното разнообразие от възли, всеки от които е малко по-различен, сякаш е отражение на различните свойства на многото химични елементи. Стабилността на вихровите пръстени може да осигури и постоянството, от което се нуждаят атомите.
Теорията за вихрите набира популярност в научната общност и вдъхновява Тейт да започне да съставя таблици на всички възли, създавайки нещо, което се надява да бъде равносилно на таблица на елементите. Разбира се, атомите не са възли и не съществува етер. В края на 80-те години на XIX в. Томсън постепенно се отказва от теорията си за вихрите, но по това време Тейт е завладян от математическата елегантност на своите възли и продължава проекта си за съставяне на таблици. В този процес той създава математическата област на теорията на възлите.
Всички сме запознати с възлите - те държат връзките на обувките ни, лодките - на кея, а алпинистите - на скалите под тях. Но тези възли не са точно това, което математиците (включително Тейт) биха нарекли възел. Въпреки че един заплетен кабел за удължаване може да изглежда като възел, винаги е възможно да го разплетете. За да получите математически възел, трябва да съедините свободните краища на кабела, за да образувате затворена примка.
Тъй като нишките на един възел са гъвкави като струна, математиците разглеждат теорията на възлите като подобласт на топологията, изучаваща гъвкавите форми. Понякога е възможно да разплетем възел, така че той да се превърне в прост кръг, който наричаме "разплетен възел". По-често обаче разплитането на възел е невъзможно.
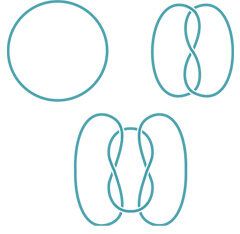 Три прости възела (отгоре наляво, по посока на часовниковата стрелка): разплетен възел, трилистна петолъчка и квадратен възел. |
Комбинирането на прост възел, наречен "трилистник", с неговия огледален образ се получава квадратен възел. |
Кредит: Merrill Sherman/Quanta Magazine; източник: David S. Richeson
Възлите могат и да се комбинират, за да образуват нови възли.
Използвайки терминология от света на числата, математиците казват, че трилистникът е прост възел, квадратният възел е съставен, а подобно на числото 1, развързаният възел не е нито един от тях. Тази аналогия е допълнително подкрепена през 1949 г., когато Хорст Шуберт доказва, че всеки възел или е прост, или може да бъде разложен еднозначно на прости възли.
Друг начин за създаване на нови възли е да преплетете два или повече възела, като образувате връзка. Прост пример за това са бормеевите пръстени, наречени така, защото са изобразени на герба на италианския род Боромео.
 За да се образуват бормеевите пръстени, се преплитат три пръстена, въпреки че няма два отделни кръга, които да са свързани. Кредит: Merrill Sherman/Quanta Magazine За да се образуват бормеевите пръстени, се преплитат три пръстена, въпреки че няма два отделни кръга, които да са свързани. Кредит: Merrill Sherman/Quanta Magazine |
 Бормеевите пръстени са изобразени на герба на италианския род Боромео (на син фон). Бормеевите пръстени са изобразени на герба на италианския род Боромео (на син фон). |
Томсън и Тейт не са първите, които разглеждат възлите по математически начин. Още през 1794 г. Карл Фридрих Гаус пише и рисува примери за възли в личния си бележник. Ученикът на Гаус Йохан Листинг пише за възлите в монографията си от 1847 г. Vorstudien zur Topologie ("Предварителни изследвания по топология"), откъдето произлиза и терминът топология.
Но Тейт е първият учен, който работи върху това, което се превръща в основен проблем в теорията на възлите: класификацията и съставянето на таблици на всички възможни възли. В продължение на години на упорита работа, използвайки единствено геометричната си интуиция, той открива и класифицира всички прости възли, които, проектирани върху равнина, имат най-много седем пресечни точки.
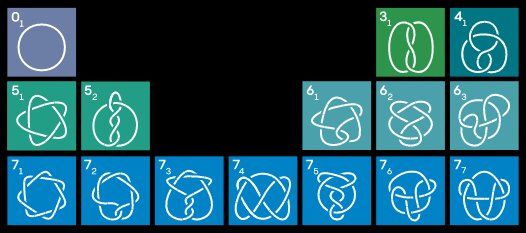
Развързаният възел и всички прости възли със седем или по-малко пресичания (без да се вземат предвид огледалните образи), подредени в стила на периодичната таблица. Кредит: Merrill Sherman/Quanta Magazine
В края на XIX век Тейт научава, че двама други души - преподобният Томас Къркман и американският математик Чарлз Литъл - също изучават този проблем. Със съвместните си усилия те класифицират всички прости възли с до 10 пресичания и много от тези с 11 пресичания. Удивително е, че техните таблици до 10 са пълни: В тях не е пропуснат нито един възел.
Забележително е, че Тейт, Къркман и Литъл са постигнали толкова много без теоремите и техниките, които ще бъдат открити през следващите години. Но едно нещо, което работи в тяхна полза, е фактът, че повечето малки възли са "алтерниращи" или "редуващи се", което означава, че имат проекция, в която пресичанията се редуват - под, над, под, над и т.н. по протежение на всеки компонент, т.е. показват последователен модел на пресичане.
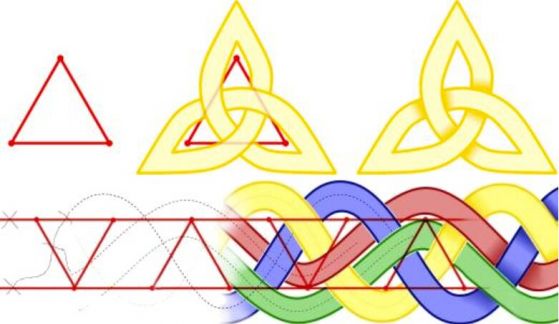
Примери на алтерниращи възли, свързани с плосък граф. Възелът на трилистника е свързан с триъгълник. Кредит: Wikimedia Commons
Алтерниращите възли имат свойства, които ги правят по-лесни за класифициране от неалтерниращите възли. Например намирането на минималния брой пресичания за всяка проекция на възел е трудно. Но Тейт, който години наред погрешно е смятал, че всички възли са алтерниращи, е измислил начин да се разбере дали е намерен този минимален брой: ако в проекцията на един алтерниращ възел няма пресичания, които могат да бъдат премахнати чрез обръщане на част от възела, то това трябва да е проекцията с минимален брой пресичания.
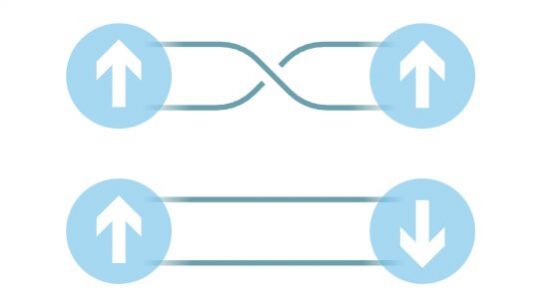
Тейт нарича всяко пресичане, което може да бъде премахнато чрез обръщане на част от възела, "самостойно" или несъществено. Кредит: Merrill Sherman/Quanta Magazine.
Това и още две от предположенията на Тейт за редуващите се възли се оказват верни. Въпреки това тези известни предположения са доказани едва в края на 80-те и началото на 90-те години на миналия век с помощта на математически инструмент, разработен през 1984 г. от Вон Джоунс (Vaughan Jones), който е носител на медал "Фийлдс" за работата си в областта на теорията на възлите.
За съжаление, редуването на възли може да ви помогне само донякъде. Щом навлезем във възли с осем или повече пресичания, броят на неалтерниращите възли нараства бързо, което прави техниките на Тейт по-малко полезни.

Този възел с осем пресичания, начертан като възел на истинския влюбен, не може да бъде начертан с редуваща се проекция. Кредит: Merrill Sherman/Quanta Magazine
Първоначалната таблица на всички възли с 10 кръстосвания е била пълна, но Тейт, Къркман и Литъл са направили двойно преброяване. Едва през 70-те години на миналия век Кенет Перко (Kenneth Perko), адвокат, който изучавал теория на възлите в Принстън, забелязва, че два от възлите са огледални образи един на друг. Сега те са известни като двойката Перко в негова чест.
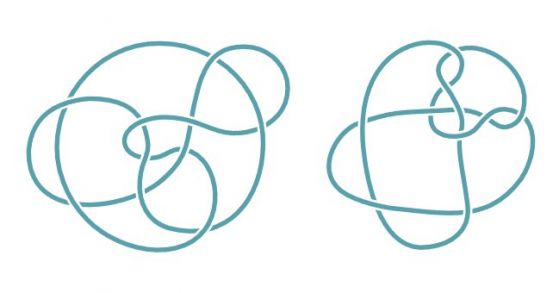
Тези два възела с 10 пресичания, известни като двойката Перко, са един и същ възел. Кредит: Merrill Sherman/Quanta Magazine
През последния век математиците са открили много хитри начини да определят дали възлите наистина са различни. По същество идеята е да се определи инвариант - свойство, величина или алгебричен обект, който е свързан с възела и често може да бъде изчислен просто. (Тези свойства имат имена като оцветеност, количество на мостовете или кривина.)
Трицветност
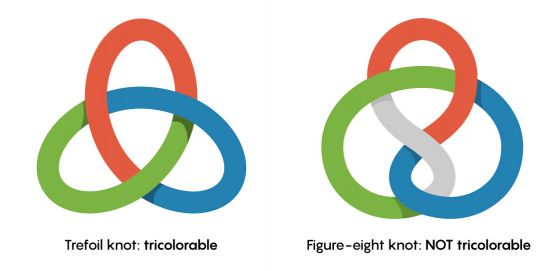
Да вземем например инвариант, наречен трицветност. Диаграмата на възел е трицветна, ако има начин да се оцветят нейните нишки в червено, синьо и зелено, така че при всяко пресичане трите нишки, които се срещат, да са или с един и същи цвят, или с различни цветове. Математиците са показали, че дори когато разместите нишките на възела, неговата трицветност (или липсата на такава) остава непроменена. С други думи, трицветността е вродена характеристика на възела.
Трицветният възел, известен като "трилистник", е трицветен. Но „невъзелът“ (примка, която няма действителни възли, дори и да изглежда заплетен) не може да бъде трицветен, предоставяйки мигновено доказателство, че трилистникът не е прикрит невъзел.
Но докато трицветността ни позволява да различим някои възли от невъзлите, тя не е перфектен инструмент за тази цел: възлите, които са трицветни, определено са завързани, но възлите, които не са трицветни, не са определено незавързани. Например, възелът "осмица" (вдясно) не може да бъде трицветен, но е истински възел. Този възел попада в "сляпото петно" на трицветността.
5W инфографика за Quanta Magazine
Въоръжени с тези етикети, математиците вече могат лесно да сравняват два възела: Ако те се различават по даден признак, значи не са един и същ възел. Нито едно от тези свойства обаче не е това, което математиците наричат пълен инвариант, което означава, че два различни възела могат да имат едно и също свойство.
Поради цялата тази сложност може би не е изненадващо, че съставянето на таблици на възлите все още продължава. Съвсем наскоро, през 2020 г., Бенджамин Бъртън класифицира всички прости възли до 19 пресечни точки (от които има почти 300 милиона).
Традиционната теория на възлите има смисъл само в рамките на три измерения: В две измерения е възможно само развързването на възел, а в четири измерения допълнителното пространство позволява на възлите да се развързват сами, така че всеки възел е тъждествен на развързания.
В четириизмерното пространство обаче можем да правим възли на сфери. За да разберете какво означава това, представете си, че нарязвате обикновена сфера на равни интервали. По този начин се получават кръгове, като линии на географската ширина - паралелите. Ако обаче разполагаме с допълнително измерение, бихме могли да направим възел на сферата, така че срезовете, сега триизмерни, а не двуизмерни, да бъдат възли.
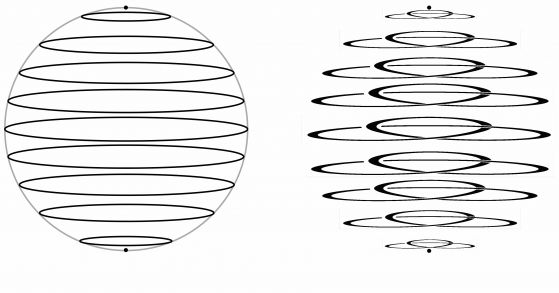
Когато нарежем сфера в триизмерното пространство, получаваме кръгове. Но парчетата от една възлова сфера в четириизмерното пространство могат да бъдат възли.
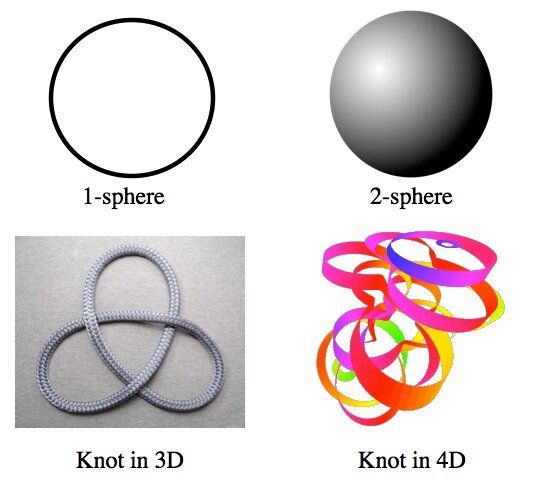
N-мерна сфера може да бъде вързана на възли в N+2 измерение. 1-мерните сфери могат да бъдат вързани на възли в три измерения (това са познатите „възли“), което означава, че същност могат да бъдат създадени. 2-мерните сфери (повърхността на кълбо) могат да бъдат вързани на възли в четири измерения. Изображението тук е само напречно сечение на такъв възел.
Тази идея стои в основата на един от най-големите скорошни резултати в теорията на възлите. През 2018 г. тогавашната аспирантка Лиза Пичирило (Lisa Piccirillo) решава задача, нерешена 50 години, за възел с 11 пресечни точки, открит за първи път от Джон Конуей. Въпросът е свързан с едно свойство, наречено "сечение на възел". Както видяхме, когато нарежем възлеста сфера в четиримерното пространство, получаваме възел в три измерения. Понякога можем да получим даден възел от гладко преплетена сфера, но за други възли сферата трябва да бъде преплетена и смачкана като лист хартия. Пичирило по същество доказва, че възелът на Конуей е от втория тип. На технически жаргон тя доказа, че той няма "гладко сечение".

Възелът на Конуей, за който Лиза Пичирило доказа, че не е гладко сечение. Кредит: Merrill Sherman/Quanta Magazine
Теорията на възлите е пресича математическия пейзаж през вековете. Тя започва като приложна област на математиката, като Томсън се опитва да използва възлите, за да разбере състава на материята. След като тази идея отшумява, тя се превръща в област на чистата математика, клон на интригуващата и все още неприложима област на топологията. Но през последните години теорията на възлите отново се превърна в приложна област на математиката, тъй като учените използват идеите на теорията на възлите, за да изследват динамиката на флуидите, електродинамиката, дългите молекулите с възли, като например ДНК, и т.н. За щастие, докато учените са били заети с изучаването на други неща, математиците са създавали каталози на възлите и инструменти за разплитане на техните тайни.
Why Mathematicians Study Knots, Quanta Magazine