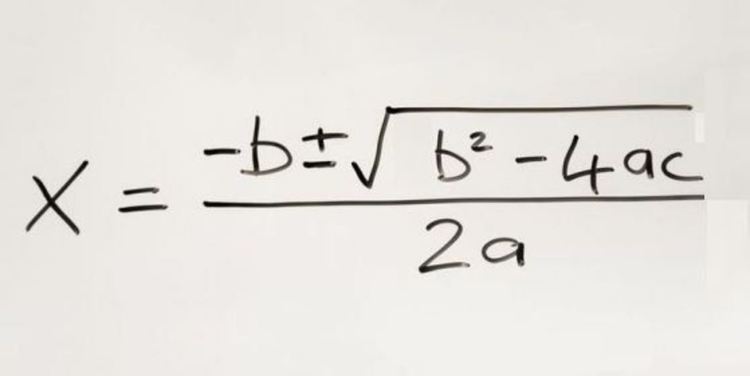Математикът д-р Po-Шън Ло измисли по-лесен начин за решаване на квадратно уравнение, съобщава MIT Technology Review.
Квадратните уравнения са полиноми, които включват x², и днес милиони хора помнят наизуст формулата за решаването на квадратно уравнение. Но малцина могат да изведат този израз.
Това се дължи и на начина, по който се преподава математика - използва се математически трик, наречен „допълване до точен квадрат“, който не е интуитивен. Досега математиците са намерили широк спектър от други начини да извлекат формулата. Но всички те също са трудни и неинтуитивни.
Така че е лесно да решим, че математиците сигурно са изчерпали проблема и не може да има по-добър начин да се извлече формулата.
Но не се оказа, че не е така.
Най-новата процедура, разработена от д-р Po-Шън Ло (Po-Shen Loh) от Университета Карнеги Мелън, заобикаля традиционните методи.
Тази задача е на повече от 4000 години и е занимавала още древните вавилонци, които е трябвало да изчислят с колко трябва да увелича размера на нивата си, за да си платят данъка. Задачата може да бъде записана като квадратно уравнение във формата Ax² + Bx + C = 0. И се решава с формулата:
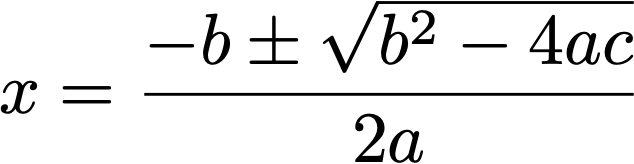
И така, д-р По-Шен Ло е намерил по-прост начин - такъв, който изглежда е останал незабелязан през последните 4000 години.
Подходът на Ло не разчита на допълване до точен квадрат или други трудни математически трикове. Всъщност е достатъчно прост за работа, което означава, че учениците изобщо не трябва да помнят формулата.
„Извеждането има потенциал да демистифицира формулата за решаване на квадратно уравнение за учениците по целия свят“, аявява д-р Ло.
Новият подход е прост. Започва с наблюдението, че ако квадратното уравнение може да се представи по следния начин:
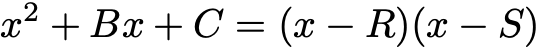
тогава дясната страна е равна на 0, когато x = R или когато x = S. Тогава това ще са корените на квадратното уравнение. Умножаването на дясната страна дава:
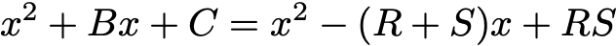
Това е вярно, когато -B = R + S и когато C = RS.
Сега тук идва най-интересното.
Ло посочва, че числата, R и S, събрани правят -B, когато средната им стойност е -B/2. "Така че търсим две числа с формата -B / 2 ± z, където z е едно неизвестно число", обяснява математикът. След това можем да умножим тези числа, за да получим C. Така че
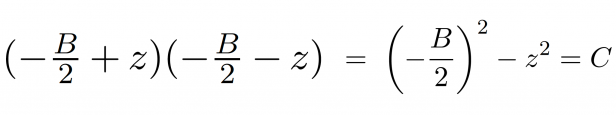
След няколко прости преобразувания получаваме:
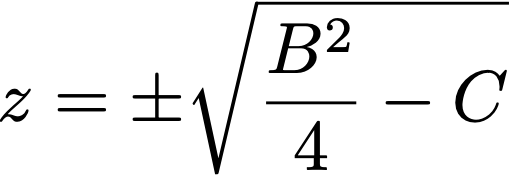
Което означава, че решението за квадратното уравнение е:
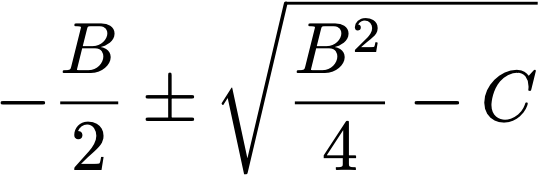
Готово! Това е формулата за решаване на квадратно уравнение.
По-общата версия може да бъде получена чрез разделяне на уравнението Ax² + Bx + C = 0 на A, за да се получи x² + B / Ax + C / A = 0 и след това се повтаря горния процес.
Това е много значително подобрение спрямо предишния метод и Ло показва защо е така с прост пример.
Намерете корените на следното квадратно уравнение: x² - 2x + 4 = 0
Традиционният метод е да се вземат стойностите за A, B и C и да се включат във формулата. Но подходът на Ло решава проблема интуитивно. Първата стъпка е да помислим, че двата корена на уравнението трябва да са равни на -B / 2 ± z = 1 ± z
И тъй като тяхното произведение трябва да е C = 4, можем да напишем:
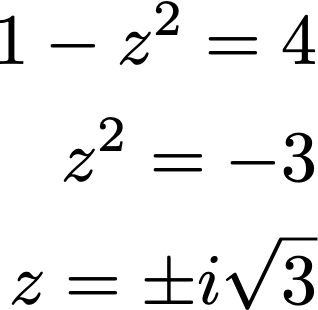
Значи корените са:
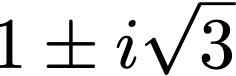
Решаването на същата задача с традиционния метод е много по-сложно. Новият подход е много по-лесен и по-интуитивен, не на последно място, защото изобщо не изисква да се запаметява формулата. Интересен въпрос е защо никой досега не се е сетил.
Ло споделя, че е ще е много изненадан, ако никой досега не е откривал този подход, предвид 4000-годишната история на тази тема и милиардите хора, които са се сблъскали с формулата и нейното доказателство. И все пак тази техника със сигурност не е широко преподавана или известна
Ло е търсил подход, подобен на неговия в цялата история на математиката, но без успех. Той е разгледал методите, разработени от древните вавилонци, китайци, гърци, индийци и араби, както и съвременните математици от Ренесанса до днес. Изглежда никой от тях не е направил тази стъпка, въпреки че Ло използва проста алгебра, позната от векове.
Така че защо чак сега? Ло смята, че е свързано с начина, по който конвенционалният подход доказва, че квадратните уравнения имат два корена.
„Може би причината е, защото всъщност математически нетривиално е да се направи обратното: винаги има два корена и тези корени имат сума -B и произведение C“, пояснява той.
Ло, който е преподавател по математика, открива своя подход, докато анализира учебните програми по математика за ученици, за да разработи нови обяснения. И така стига до новия начин на решаване.
Въпросът сега е колко широко ще се разпространи и колко бързо. Д-р Ло вярва, че учениците могат да научат този метод по-интуитивно, отчасти защото не се изисква специална отделна формула. Все още е сложно, но е по-малко сложно, особено ако д-р Ло е прав, че това ще изглади разбирането на учениците за това как работят квадратните уравнения и как се вписват в математиката.
Вижте видеото с обясненията на д-р Ло.
Справка: arxiv.org/abs/1910.06709 : A Simple Proof of the Quadratic Formula
Източник: A new way to make quadratic equations easy, MIT Technology Review